树形结构数据库表Schema设计的两种方案
前言
程序设计过程中,我们常常用树形结构来表征某些数据的关联关系,如企业上下级部门、栏目结构、商品分类等等,通常而言,这些树状结构需要借助于数据库完成持久化。然而目前的各种基于关系的数据库,都是以二维表的形式记录存储数据信息,因此是不能直接将tree存入dbms,设计合适的schema及其对应的crud算法是实现关系型数据库中存储树形结构的关键。
理想中树形结构应该具备如下特征:数据存储冗余度小、直观性强;检索遍历过程简单高效;节点增删改查crud操作高效。无意中在网上搜索到一种很巧妙的设计,原文是英文,看过后感觉有点意思,于是便整理了一下。本文将介绍两种树形结构的schema设计方案:一种是直观而简单的设计思路,另一种是基于左右值编码的改进方案。
一、基本数据
本文列举了一个食品族谱的例子进行讲解,通过类别、颜色和品种组织食品,树形结构图如下:
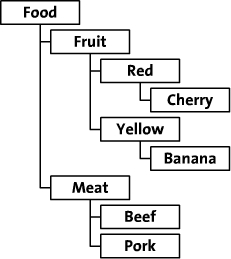
二、继承关系驱动的schema设计
对树形结构最直观的分析莫过于节点之间的继承关系上,通过显示地描述某一节点的父节点,从而能够建立二维的关系表,则这种方案的tree表结构通常设计为:{node_id,parent_id},上述数据可以描述为如下图所示:
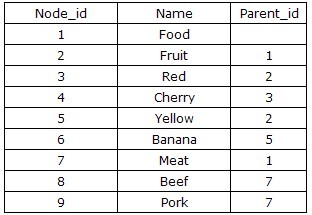
这种方案的优点很明显:设计和实现自然而然,非常直观和方便。缺点当然也是非常的突出:由于直接地记录了节点之间的继承关系,因此对tree的任何crud操作都将是低效的,这主要归根于频繁的“递归”操作,递归过程不断地访问数据库,每次数据库io都会有时间开销。当然,这种方案并非没有用武之地,在tree规模相对较小的情况下,我们可以借助于缓存机制来做优化,将tree的信息载入内存进行处理,避免直接对数据库io操作的性能开销。
三、基于左右值编码的schema设计
在基于数据库的一般应用中,查询的需求总要大于删除和修改。为了避免对于树形结构查询时的“递归”过程,基于tree的前序遍历设计一种全新的无递归查询、无限分组的左右值编码方案,来保存该树的数据。
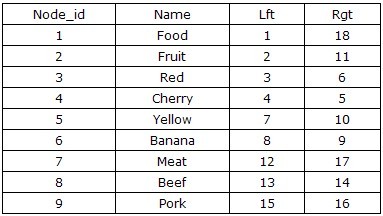
第一次看见这种表结构,相信大部分人都不清楚左值(lft)和右值(rgt)是如何计算出来的,而且这种表设计似乎并没有保存父子节点的继承关系。但当你用手指指着表中的数字从1数到18,你应该会发现点什么吧。对,你手指移动的顺序就是对这棵树进行前序遍历的顺序,如下图所示。当我们从根节点food左侧开始,标记为1,并沿前序遍历的方向,依次在遍历的路径上标注数字,最后我们回到了根节点food,并在右边写上了18。
第一次看见这种表结构,相信大部分人都不清楚左值(lft)和右值(rgt)是如何计算出来的,而且这种表设计似乎并没有保存父子节点的继承关系。但当你用手指指着表中的数字从1数到18,你应该会发现点什么吧。对,你手指移动的顺序就是对这棵树进行前序遍历的顺序,如下图所示。当我们从根节点food左侧开始,标记为1,并沿前序遍历的方向,依次在遍历的路径上标注数字,最后我们回到了根节点food,并在右边写上了18。
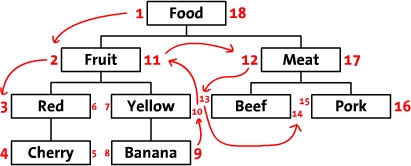
依据此设计,我们可以推断出所有左值大于2,并且右值小于11的节点都是fruit的后续节点,整棵树的结构通过左值和右值存储了下来。然而,这还不够,我们的目的是能够对树进行crud操作,即需要构造出与之配套的相关算法。
四、树形结构crud算法
(1)获取某节点的子孙节点
只需要一条sql语句,即可返回该节点子孙节点的前序遍历列表,以fruit为例:select* from tree where lft between 2 and 11 order by lft asc。查询结果如下所示:
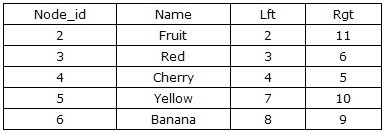
那么某个节点到底有多少的子孙节点呢?通过该节点的左、右值我们可以将其子孙节点圈进来,则子孙总数 = (右值 – 左值– 1) / 2,以fruit为例,其子孙总数为:(11 –2 – 1) / 2 = 4。同时,为了更为直观地展现树形结构,我们需要知道节点在树中所处的层次,通过左、右值的sql查询即可实现,以fruit为例:selectcount(*) from tree where lft <= 2 and rgt >=11。为了方便描述,我们可以为tree建立一个视图,添加一个层次数列,该列数值可以写一个自定义函数来计算,函数定义如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
create function dbo.countlayer
(
@node_id int
)
returns int
as
begin
declare @result int
set @result = 0
declare @lft int
declare @rgt int
if exists(select node_id from tree where node_id = @node_id)
begin
select @lft = lft, @rgt = rgt from tree where node_id = @node_id
select @result = count(*) from tree where lft <= @lft and rgt >= @rgt
end
return @result
end
go
|
基于层次计算函数,我们创建一个视图,添加了新的记录节点层次的数列:
|
1
2
3
4
|
create view dbo.treeview
as
select node_id, name, lft, rgt, dbo.countlayer(node_id) as layer from dbo.tree order by lft
go
|
创建存储过程,用于计算给定节点的所有子孙节点及相应的层次:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
create procedure [dbo].[getchildrennodelist]
(
@node_id int
)
as
declare @lft int
declare @rgt int
if exists(select node_id from tree where node_id = @node_id)
begin
select @lft = lft, @rgt = rgt from tree where node_id = @node_id
select * from treeview where lft between @lft and @rgt order by lft asc
end
go
|
现在,我们使用上面的存储过程来计算节点fruit所有子孙节点及对应层次,查询结果如下:
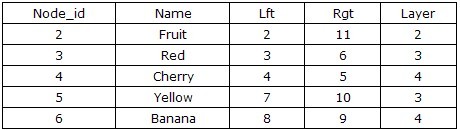
从上面的实现中,我们可以看出采用左右值编码的设计方案,在进行树的查询遍历时,只需要进行2次数据库查询,消除了递归,再加上查询条件都是数字的比较,查询的效率是极高的,随着树规模的不断扩大,基于左右值编码的设计方案将比传统的递归方案查询效率提高更多。当然,前面我们只给出了一个简单的获取节点子孙的算法,真正地使用这棵树我们需要实现插入、删除同层平移节点等功能。
(2)获取某节点的族谱路径
假定我们要获得某节点的族谱路径,则根据左、右值分析只需要一条sql语句即可完成,以fruit为例:select* from tree where lft < 2 and rgt > 11 order by lft asc ,相对完整的存储过程:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
create procedure [dbo].[getparentnodepath]
(
@node_id int
)
as
declare @lft int
declare @rgt int
if exists(select node_id from tree where node_id = @node_id)
begin
select @lft = lft, @rgt = rgt from tree where node_id = @node_id
select * from treeview where lft < @lft and rgt > @rgt order by lft asc
end
go
|
(3)为某节点添加子孙节点
假定我们要在节点“red”下添加一个新的子节点“apple”,该树将变成如下图所示,其中红色节点为新增节点。
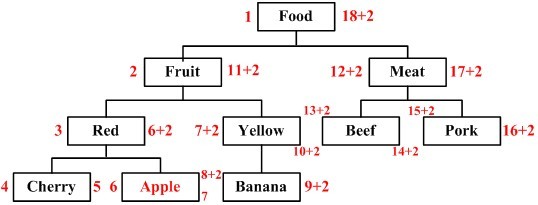
仔细观察图中节点左右值变化,相信大家都应该能够推断出如何写sql脚本了吧。我们可以给出相对完整的插入子节点的存储过程:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
create procedure [dbo].[addsubnode]
(
@node_id int,
@node_name varchar(50)
)
as
declare @rgt int
if exists(select node_id from tree where node_id = @node_id)
begin
set xact_abort on
begin transction
select @rgt = rgt from tree where node_id = @node_id
update tree set rgt = rgt + 2 where rgt >= @rgt
update tree set lft = lft + 2 where lft >= @rgt
insert into tree(name, lft, rgt) values(@node_name, @rgt, @rgt + 1)
commit transaction
set xact_abort off
end
go
|
(4)删除某节点
如果我们想要删除某个节点,会同时删除该节点的所有子孙节点,而这些被删除的节点的个数为:(被删除节点的右值 – 被删除节点的左值+ 1) / 2,而剩下的节点左、右值在大于被删除节点左、右值的情况下会进行调整。来看看树会发生什么变化,以beef为例,删除效果如下图所示。
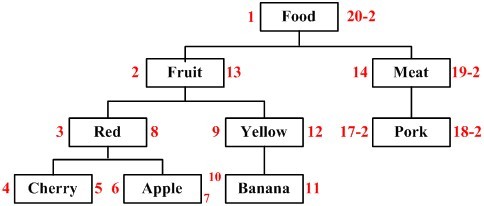
则我们可以构造出相应的存储过程:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
create procedure [dbo].[delnode]
(
@node_id int
)
as
declare @lft int
declare @rgt int
if exists(select node_id from tree where node_id = @node_id)
begin
set xact_abort on
begin transction
select @lft = lft, @rgt = rgt from tree where node_id = @node_id
delete from tree where lft >= @lft and rgt <= @rgt
update tree set lft = lft – (@rgt - @lft + 1) where lft > @lft
update tree set rgt = rgt – (@rgt - @lft + 1) where rgt > @rgt
commit transaction
set xact_abort off
end
go
|
五、总结
我们可以对这种通过左右值编码实现无限分组的树形结构schema设计方案做一个总结:
(1)优点:在消除了递归操作的前提下实现了无限分组,而且查询条件是基于整形数字的比较,效率很高。
(2)缺点:节点的添加、删除及修改代价较大,将会涉及到表中多方面数据的改动。
当然,本文只给出了几种比较常见的crud算法的实现,我们同样可以自己添加诸如同层节点平移、节点下移、节点上移等操作。有兴趣的朋友可以自己动手编码实现一下,这里不在列举了。值得注意的是,实现这些算法可能会比较麻烦,会涉及到很多条update语句的顺序执行,如果顺序调度考虑不周详,出现bug的话将会对整个树形结构表产生惊人的破坏。因此,在对树形结构进行大规模修改的时候,可以采用临时表做中介,以降低代码的复杂度,同时,强烈推荐在做修改之前对表进行完整备份,以备不时之需。在以查询为主的绝大多数基于数据库的应用系统中,该方案相比传统的由父子继承关系构建的数据库schema更为适用。
到此这篇关于树形结构数据库表schema设计方案的文章就介绍到这了,更多相关树形结构数据库表schema设计内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持!
参考文献:《storing hierarchical data in a database article》
原文链接:https://blog.csdn.net/monkey_d_meng/article/details/6647488
本文由主机测评网发布,不代表主机测评网立场,转载联系作者并注明出处:https://zhujiwo.jb51.net/shujuku/2724.html

